This time, we will introduce the Digital Pulse Processor (DPP), which digitizes waveforms for analysis.

There are various types of waveforms, ranging from logic waveforms like TTL to pulse waveforms from radiation detectors. The pulse widths also vary, from several milliseconds to several microseconds, and even down to nanoseconds.

Digital Pulse Processors are particularly well-suited for analyzing high-speed pulse waveforms, such as those from radiation detectors—especially scintillation detectors—ranging from several hundred nanoseconds to a few nanoseconds.

In this report, we will use the APV8104-14, one of our many Digital Pulse Processor products, equipped with a 1Gsps, 14-bit ADC. We will briefly explain the process from signal input to digital pulse processing, and then focus on explaining the QDC (Charge Digital Converter).

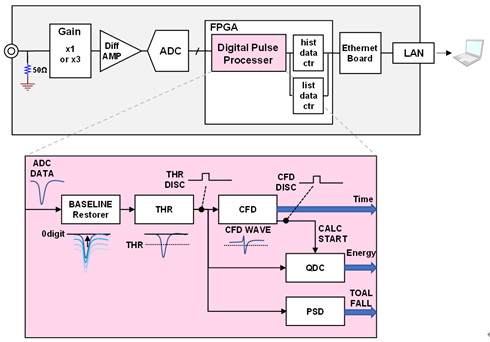
The input waveform is received with a 50Ω input impedance. The amplitude of the waveform is adjusted using gain from a high-speed amplifier circuit or an attenuator, and then digitized by the ADC.

The digitized waveform is digitally processed within the FPGA, allowing extraction of energy information (QDC), timing information (TDC), and pulse shape discrimination information (PSD). This information is useful for various physical measurement experiments. Let’s take a closer look at the signal processing section within the FPGA.

The internal signal processing is divided into several modules:
the Threshold Discriminator module, which serves as the starting point of signal processing; the CFD module for obtaining high-precision timing information; the QDC module for energy information; and the PSD module for pulse shape discrimination.

Each module performs calculations using FPGA’s characteristic parallel processing and pipeline processing. Although some latency occurs due to pipeline processing, the system can handle high-rate signal inputs with minimal dead time.

The parameters that can be set for each module are as follows.

Here, Q_s represents the total charge injected between t = 0 and t = t_q.

Similarly, the Laplace transform of the transfer function of the charge sensitive amplifier is given by the following equation:

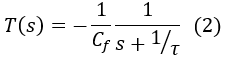
The equation for the output voltage is as follows:

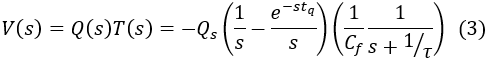
Furthermore, assuming that t_q << τ, the equation can be simplified as follows:

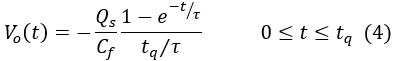
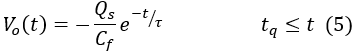
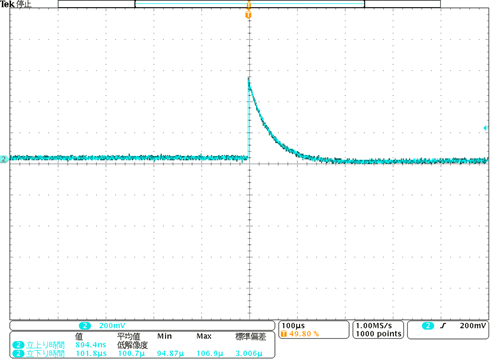
Fig. 2: Output of the Charge Sensitive Amplifier

The most important element in the charge sensitive amplifier is a JFETwhich are used in the first stage.

For example, while low-noise bipolar transistors have a lower noise voltage density than JFETs, they require base current, which increases parallel noise in the configuration of a charge amplifier with high input impedance, leading to worsened overall noise compared to FETs. Therefore, they are excluded from selection.

For operational amplifiers, JFET-input types are available, but their noise performance is inferior to that of the JFET alone. However, the circuit is very simple, making them suitable for measurements where noise is not a primary concern.

MOSFETs cannot be used due to their high 1/f noise and a noise corner frequency ranging from 10 kHz to 1 MHz.

The JFET does not require gate current, which allows for a larger feedback resistor (R_f). Additionally, the noise corner is low, ranging from 100 Hz to 1 kHz, which is sufficiently low for the operating range of 10 kHz to 10 MHz.
In terms of low noise performance, the first stage JFET is particularly critical, and a device with high transconductance (gm) and low input capacitance (Ciss) is selected. The first stage is received by an emitter-coupled folded cascode circuit. The folded cascode increases the dynamic range and achieves higher impedance.

1) gm (transconductance) and input capacitance (Ciss) of the first-stage FET

gm (transconductance) can be adjusted by the I_D drain current.

The higher the drain current, the greater the gm, but this also leads to an increase in power consumption, which can be a limitation in multi-channel systems or battery-operated devices.

The equivalent noise resistance of the FET is given by R_FET ≒ 1/gm, so generally, a higher gm results in lower noise. Therefore, products that carefully select JFETs exist for this reason.

Ciss is the input capacitance of the FET, which significantly impacts the input capacitance (C_i) of the charge sensitive amplifier.

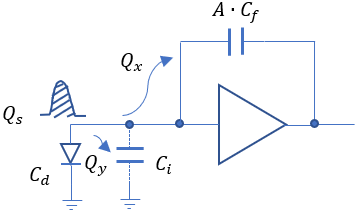
The generated charge, Q_S, is distributed and flows into Q_x and Q_y. To improve the signal-to-noise ratio (S/N), the open-loop gain A should be made as large as possible to direct the charge into A·C_f. Since C_f is also the voltage conversion gain, it cannot be made arbitrarily large. By minimizing C_i, the distribution of charge to Q_x can be maximized.

The charge flowing into Q_y is directed into the detector capacitance (C_d) and the input capacitance (C_i) of the charge sensitive amplifier, which degrades the signal-to-noise ratio (S/N).

When the detector capacitance is small, it is important to minimize C_i as much as possible. When the detector capacitance is large, it is necessary to increase gm to reduce noise. Additionally, FETs with small Ciss have faster rise-time characteristics.

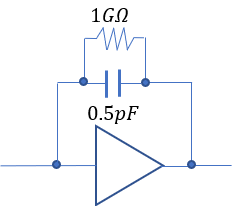
2) Feedback Capacitor (Cf) and Feedback Resistor (Rf)

Let the energy be E, the generated charge be Q, the detector's capacitance be C_d, the input capacitance of the charge sensitive amplifier be C_i, and the feedback resistor be R_f.

When the open-loop gain A is sufficiently large, the value will become constant, determined by the feedback capacitor C_f.

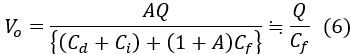
The output charge Q corresponding to the actual radiation energy is given by the following equation:

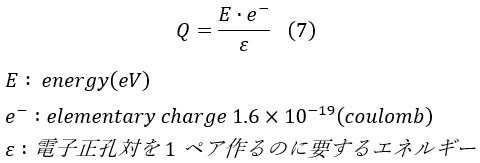
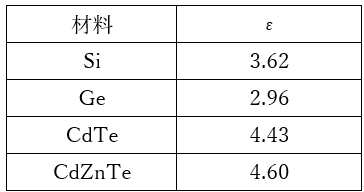
ε: The energy required to create one electron-hole pair.

The output voltage per 1 MeV, when the feedback capacitor Cf is 0.5 pF in a Si semiconductor detector, is as follows:

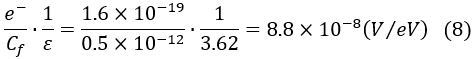
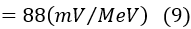
When the feedback capacitor C_f is 1 pF, the output is 44 mV, and when C_f is 2 pF, the output decreases to 22 mV. To improve the signal-to-noise ratio (S/N), it is important to select the smallest possible C_f.

The larger the feedback resistor R_f, the lower the noise. Here, we will consider the noise of the CR parallel resistor.

The admittance of the CR parallel resistor is:

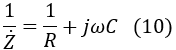
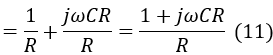
Rearranging equation (11) to express the impedance, we get:

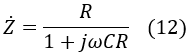
Rearranging equation (12) with the imaginary unit j, we get:

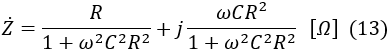
The real part of equation (13) represents the resistive component.
Therefore, the equivalent resistance R^X of the CR parallel circuit is:

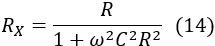
The thermal noise voltage of the resistor, Vn, is:

B: Bandwidth 　T: Tempature 300[k]　(27℃)

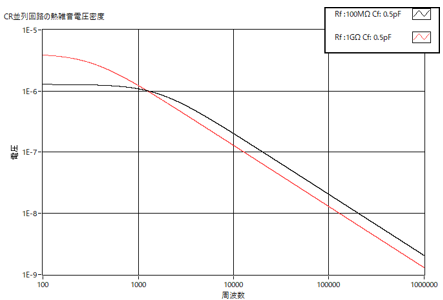
From equations (14) and (15), let's compare the case where the feedback resistor R_f is 100 MΩ and the feedback capacitor C_f is 0.5 pF, with the case where the feedback resistor R_f is 1 GΩ and the feedback capacitor C_f is 0.5 pF.

In the low-frequency region up to around 1 kHz, the 100 MΩ feedback resistor results in less noise. However, in the high-frequency region, the 1 GΩ feedback resistor results in lower noise.

The noise integration in the 10kHz to 1MHz range, which is critical in a charge-sensitive amplifier, is 20.3μVrms for 100MΩ and 12.8μVrms for 1GΩ.

It becomes approximately 2 3 , so there is a benefit to using 1GΩ.

3) Open Loop Gain (A)

By using a high-bandwidth operational amplifier (OP-AMP) instead of discrete components such as transistors for the middle and output stages, it is possible to miniaturize the design.

The circuit configuration consists of an emitter-grounded folded cascode combined with an OP-AMP, targeting open loop gains in the range of several thousand to tens of thousands.

When selecting an OP-AMP, an important performance factor to consider is the open loop gain. With a single FET, the open loop gain is only around 10 to 50 times, so ideally, we want a gain of over 300 times at 1 MHz. While noise characteristics are determined primarily by the first-stage FET, there is no particular need to focus on them, but personally, I tend to select low-noise OP-AMPS. High-bandwidth OP-AMPS naturally offer fast rise time characteristics.

The product APG1603 is designed with optimized parameters for gm, C_i, Cf, R_f, and A.

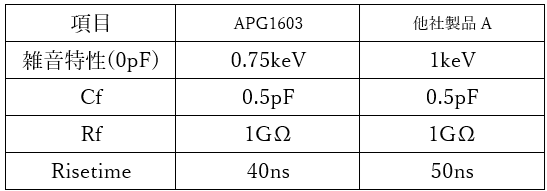
Now, let’s compare the noise characteristics of APG1603 with those of other products (with excellent noise characteristics of 1 keV) to see how much the difference in noise performance affects actual measurements.

First, below are the specifications.

First, we will test whether the catalog data is correct by using a pulser. The pulser will generate pulse heights equivalent to 1 MeV.

The Shaping amp time constant is 2μs

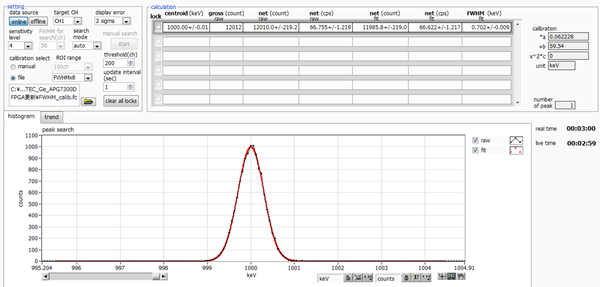
APG1603 has a pulser resolution of 0.7 keV.

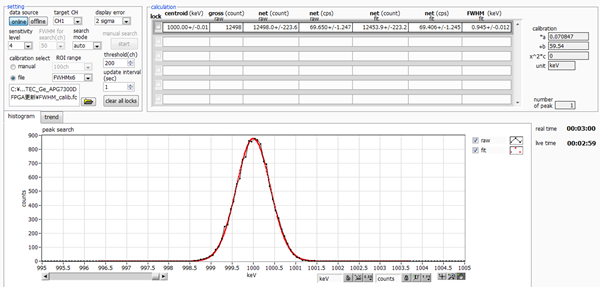
Product A from another company has a pulser resolution of 0.945 keV.

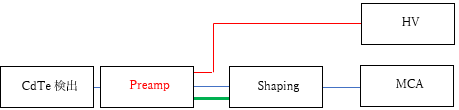
Now, we will measure the spectrum using a CdTe semiconductor detector.
The peak to be measured is the 59.5 keV peak of Am-241.

The Shaping amp time constant is 2μs

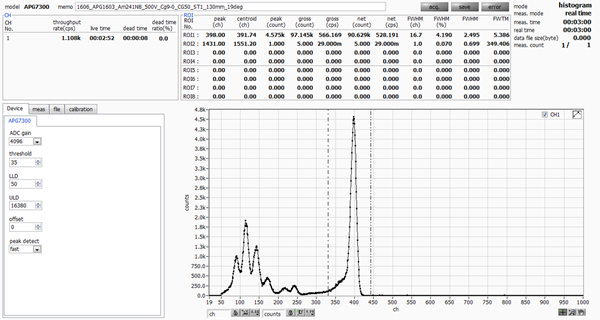
APG1603 has a resolution of 2.49 keV (4.19%) at 59.5 keV.

Product A from another company has a resolution of 3.01 keV (5.07%) at 59.5 keV.

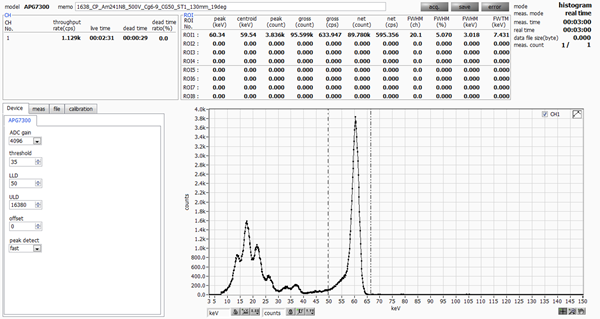
The measurement results show that APG1603 has a resolution of 2.49 keV (4.19%), while Product A from another company has a resolution of 3.01 keV (5.07%).

The difference of 0.75 keV and 1 keV in the catalog data is also reflected in the actual measurements. This can be attributed to the fact that it is a semiconductor detector and the energy of 59.5 keV is low, but we highly recommend trying APG1603.

With that, all of us at the company will continue to work hard to create better products.

We appreciate your support and encouragement.

References
[1] Okamura Michio, Interface, CQ Publishing, February 1976.
[2] Matsui Kunihiko, 100 Practical Techniques for Using OP Amps, CQ Publishing, 1999.
[3] Kowalski, Nuclear Electronics, Asakura Publishing, 1971.